Posts
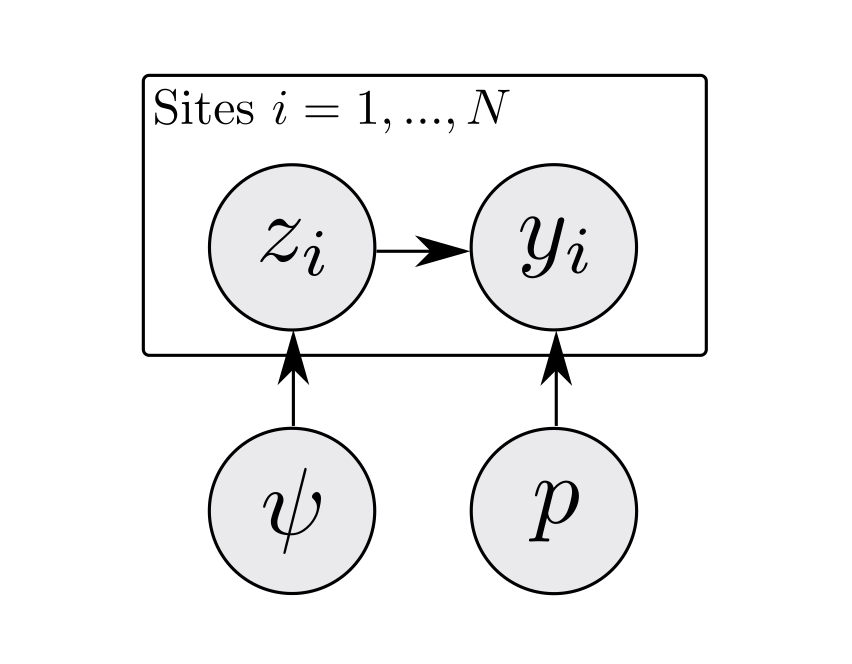
A step-by-step guide to marginalizing over discrete parameters for ecologists using Stan
Everything you might have been afraid to ask about implementing models with discrete parameters in Stan. Written for ecologists that know BUGS, JAGS, or NIMBLE, and want to use Stan. Provides an example by marginalizing over partly observed presence/absence states in a simple occupancy model.
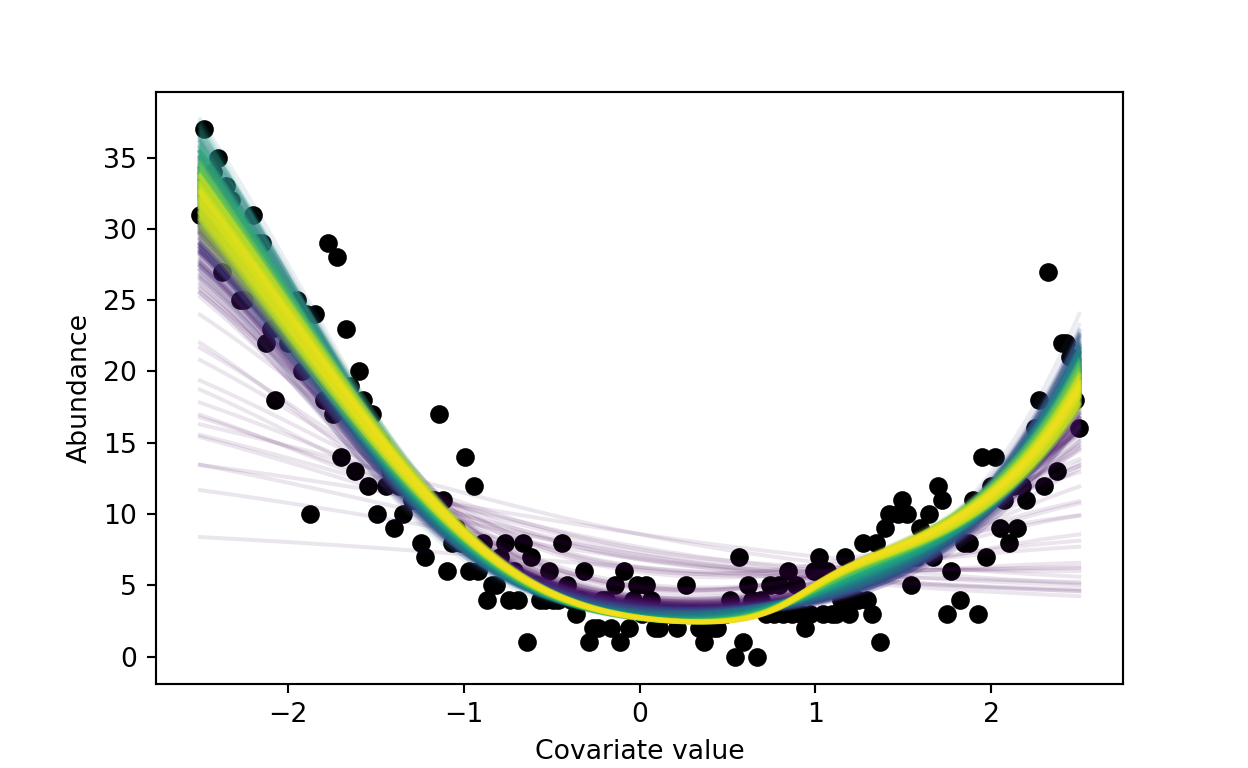
Behind the paper: Neural hierarchical models of ecological populations
A high-level overview, an example, and a call to action.

Yes, but does it (still) run?
Migrating from Jekyll to distill, with some reflections on the past 6 years.
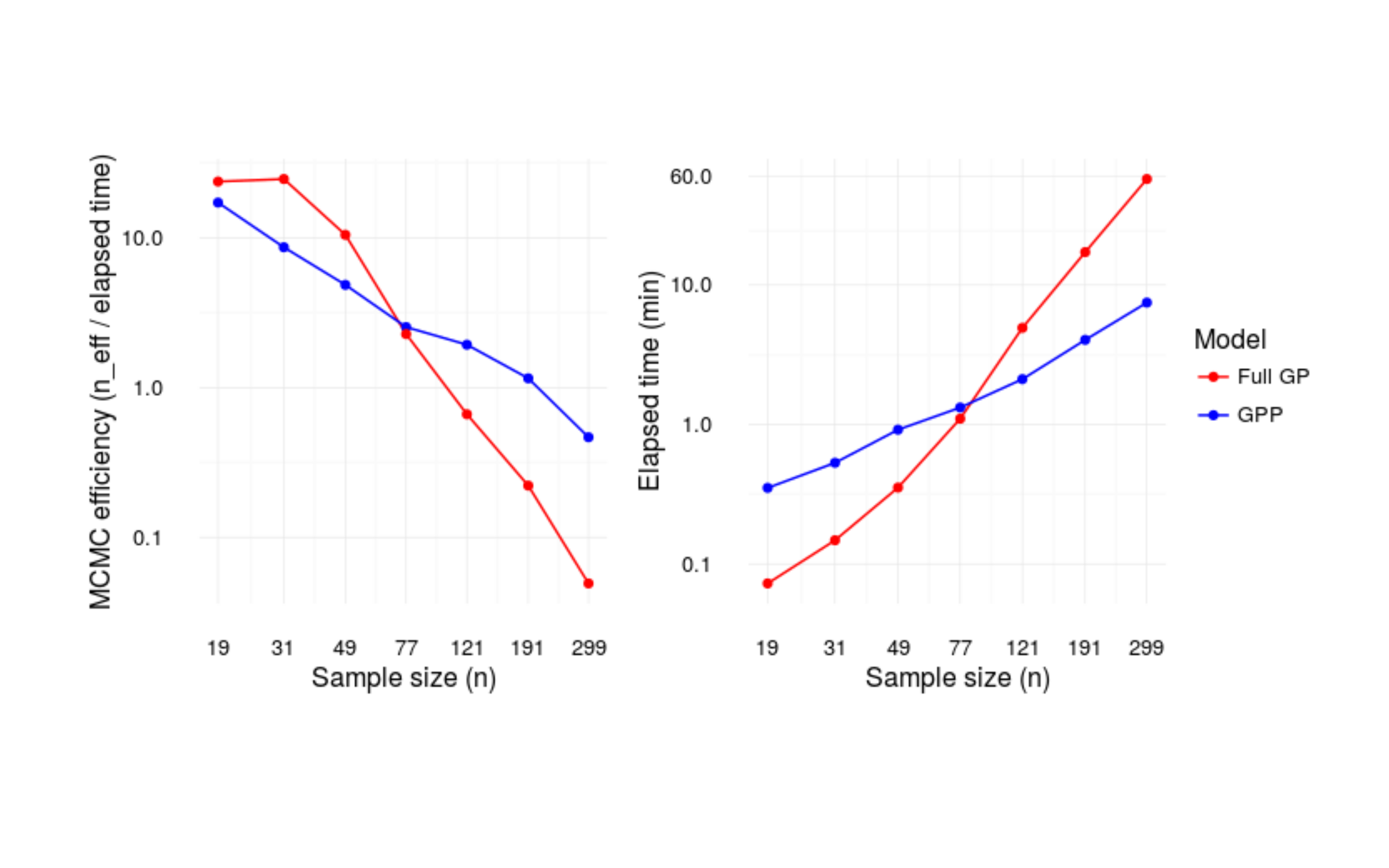
Gaussian predictive process models in Stan
Gaussian processes that scale to larger data.

The five elements ninjas approach to teaching design matrices
In-class activities to teach design matrices from multiple perspectives.

First year books
10 books I wish I had entering graduate school.

The IQUIT R video series
A series of introductory R videos.
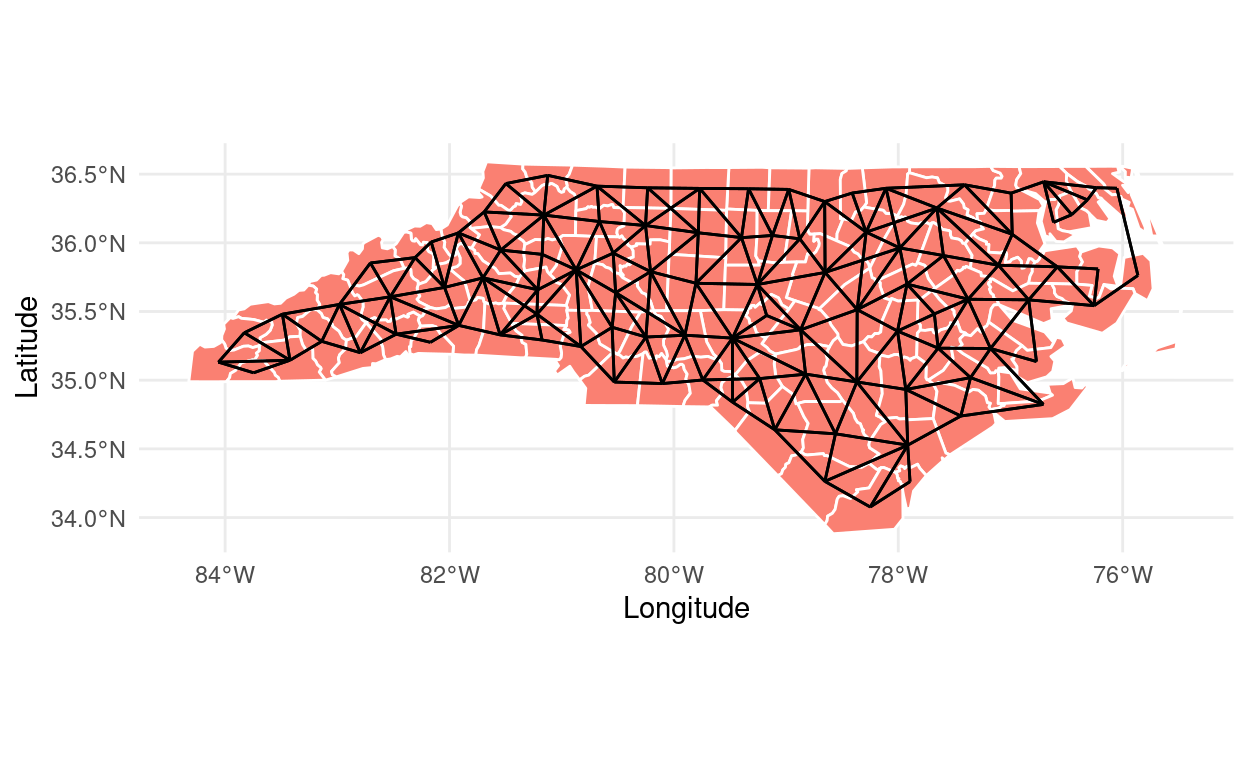
Plotting spatial neighbors in ggplot2
How to visualize spatial neighbors using ggplot2, spdep, and sf.
Why I think twice before editing plots in Powerpoint, Illustrator, Inkscape, etc.
TLDR: scripting plots is more reproducible and efficient long term

Notes on shrinkage and prediction in hierarchical models
Partial pooling and the best NBA free throw shooters of all time.
Dynamic occupancy models in Stan
Dynamic multi-year occupancy models, marginalizing over latent occurrence states.
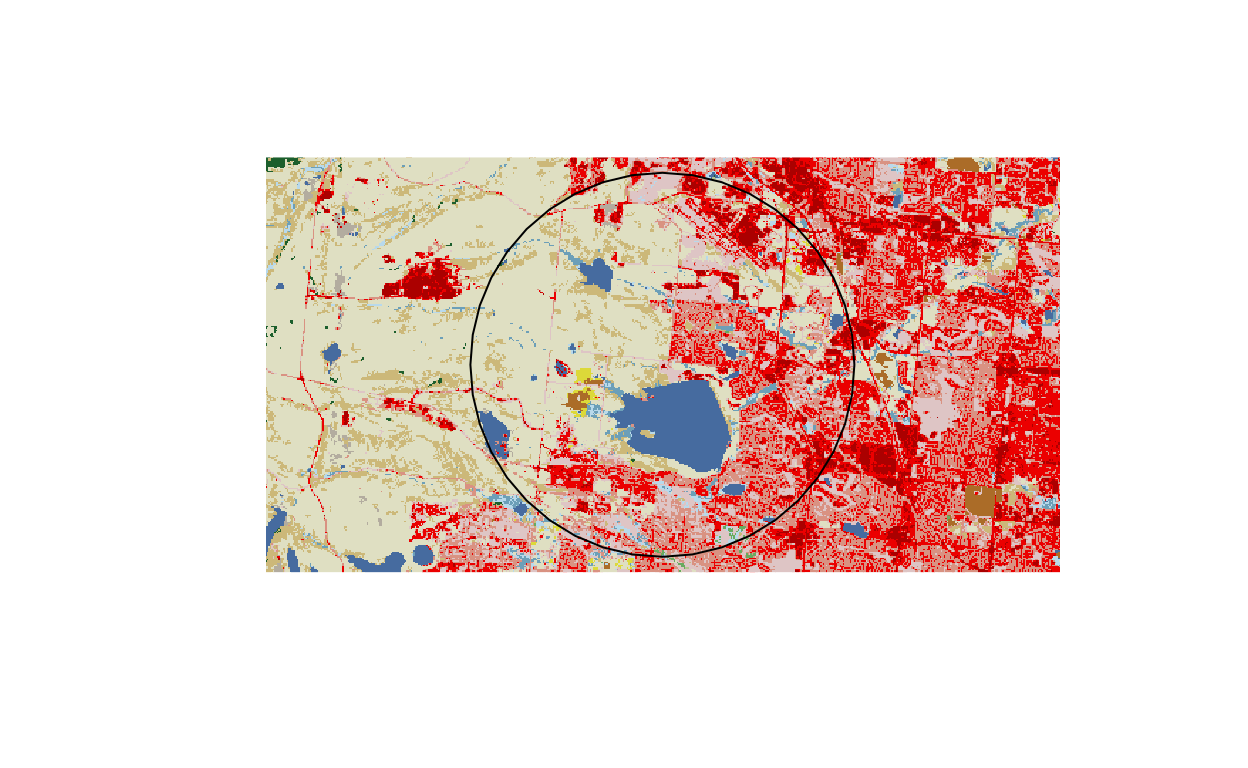
Categorical spatial data extraction around buffered points in R
Computing the proportion of land cover types using R and the raster package.
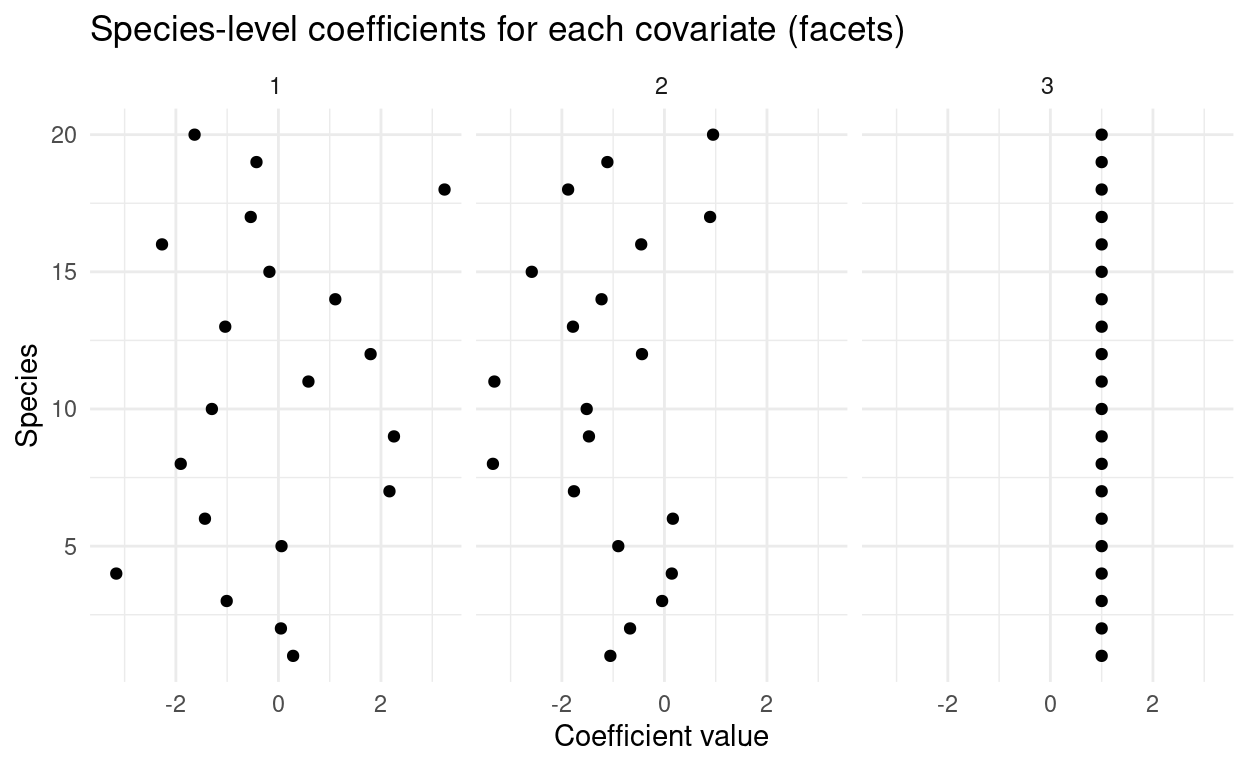
Multilevel modeling of community composition with imperfect detection
A guest post by Joe Mihaljevic.
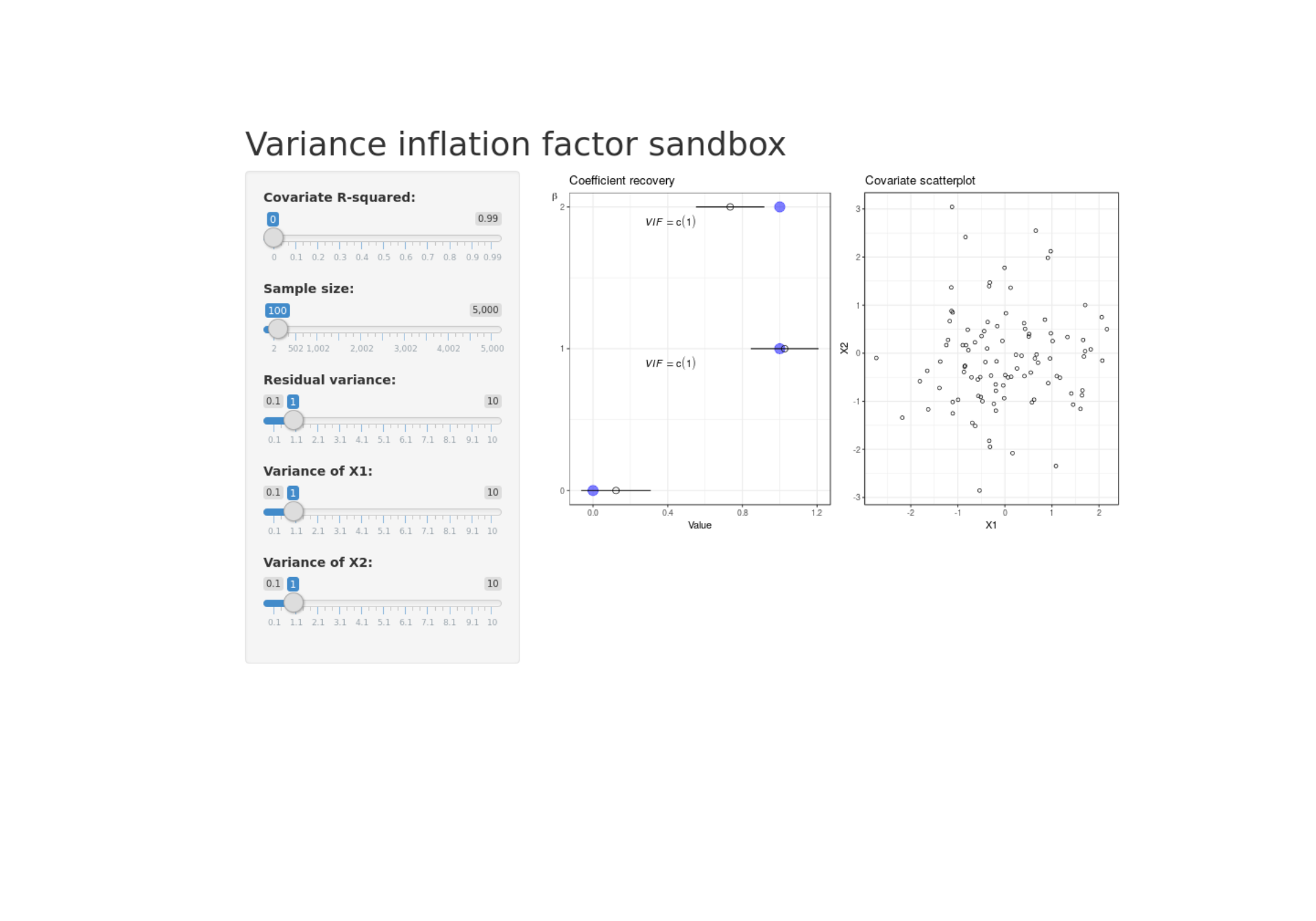
Shiny variance inflation factor sandbox
Exploring how correlation among covariates inflates uncertainty in coefficient estmates.
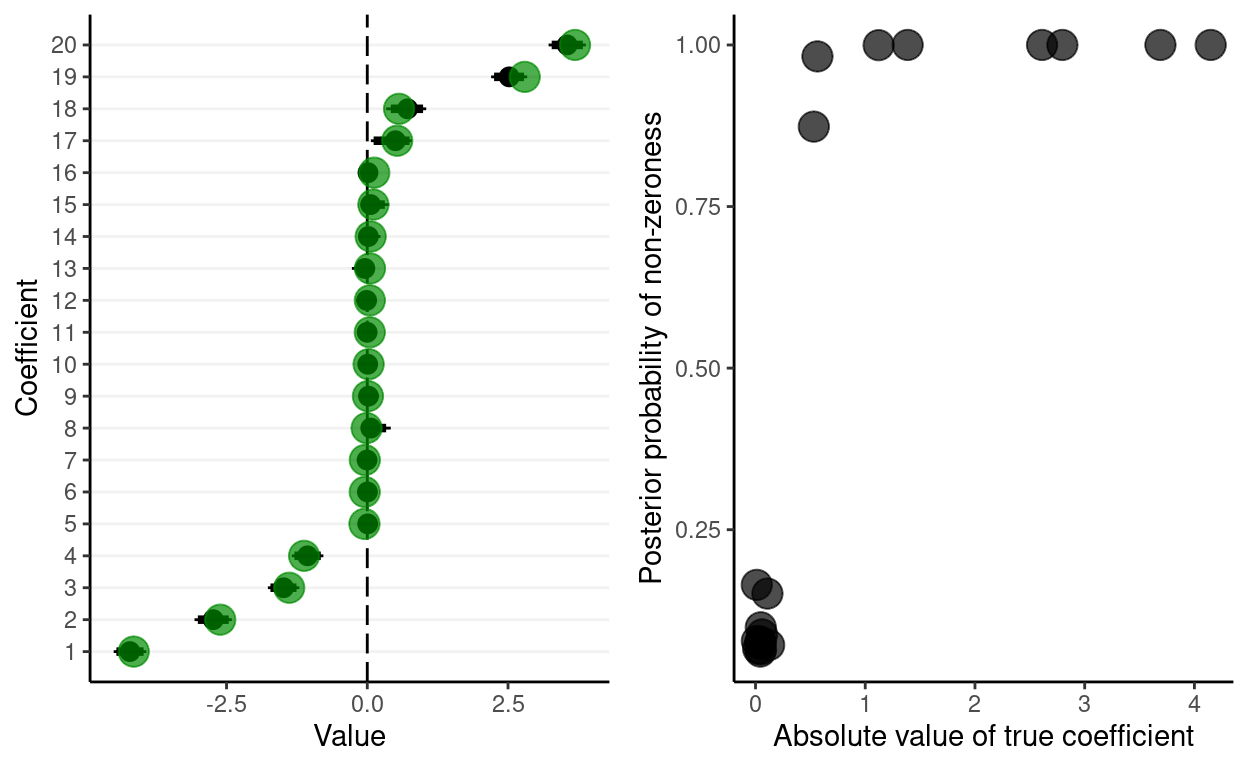
Stochastic search variable selection in JAGS
Using spike and slab priors to shrink coefficients toward zero.
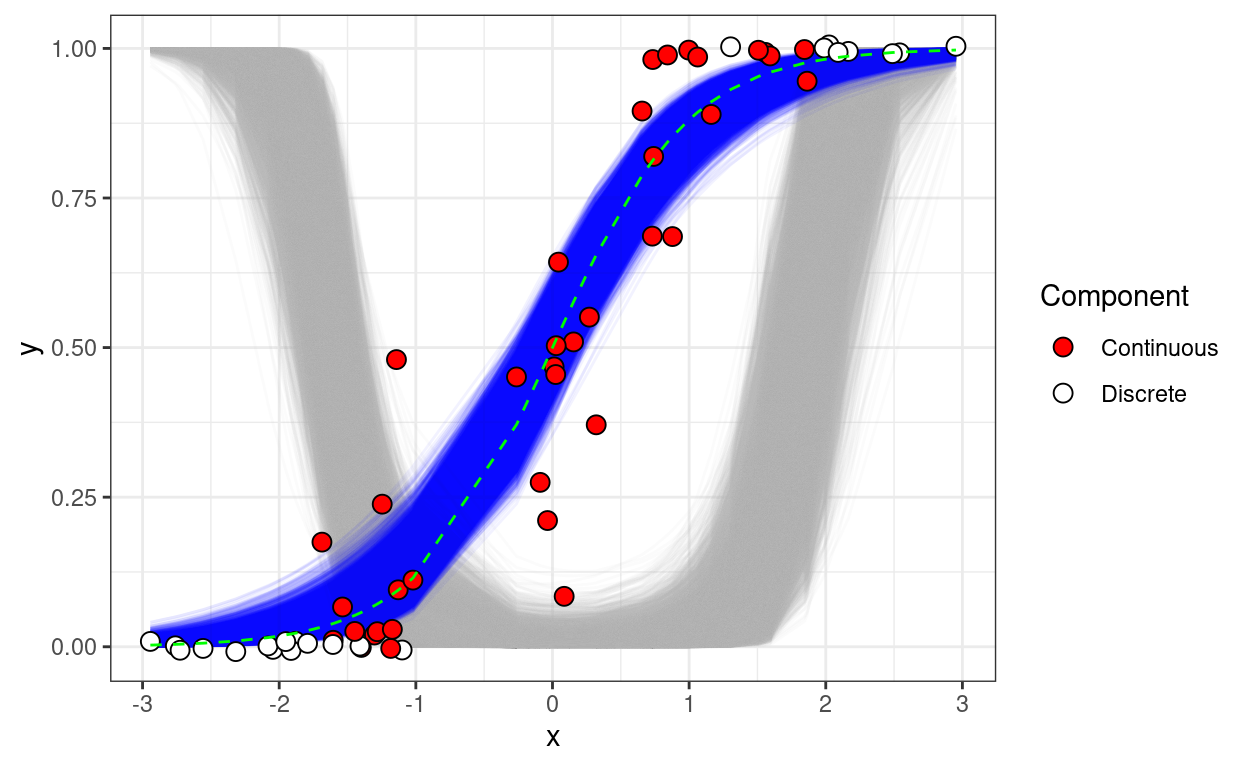
Better living through zero-one inflated beta regression
Fitting a Bayesian ZOIB regression model in JAGS.
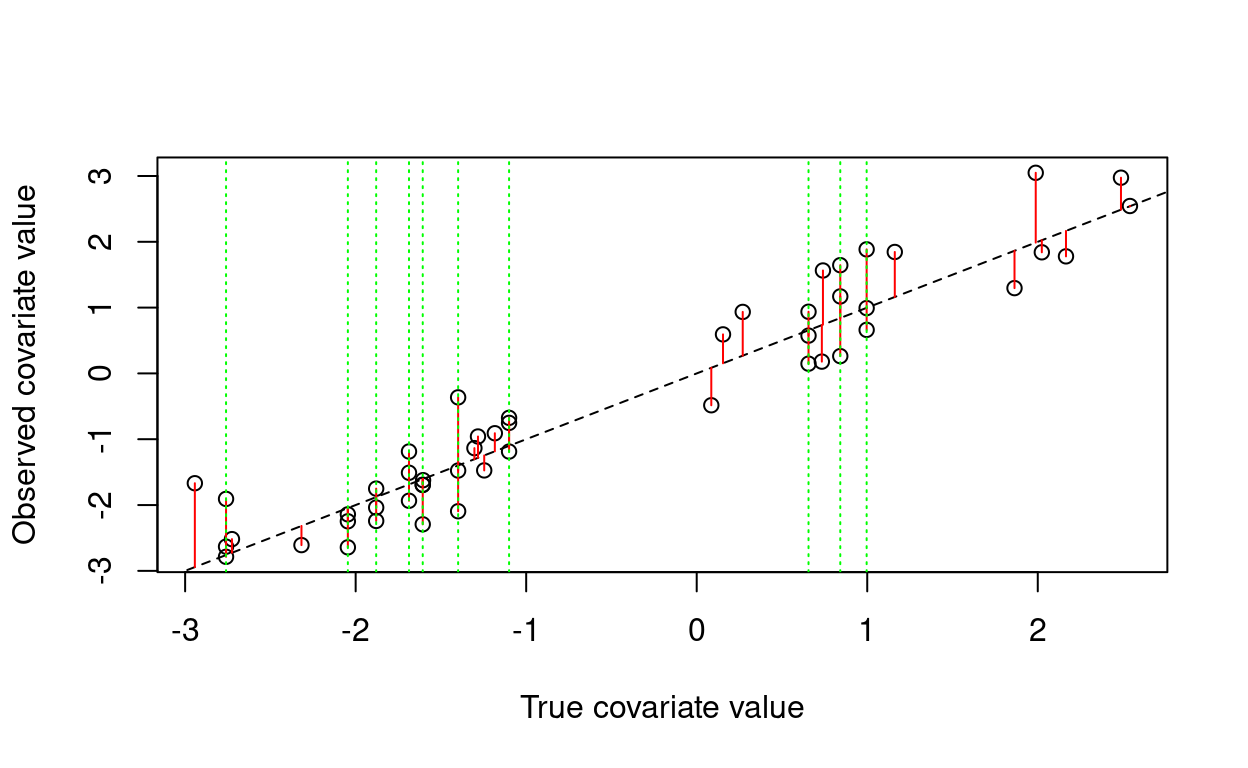
Errors-in-variables models in stan
Fitting a Bayesian regression with covariate uncertainty.

R Markdown and my divorce from Microsoft Word
A short description of the post.
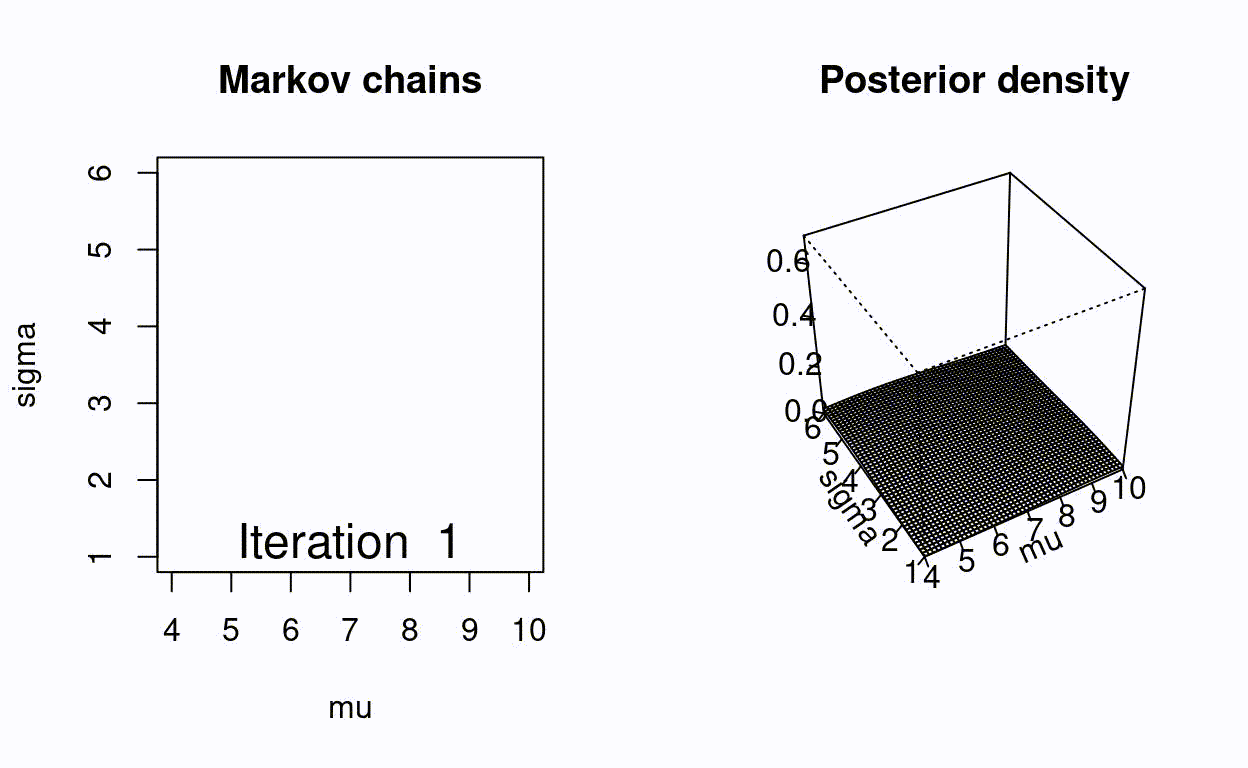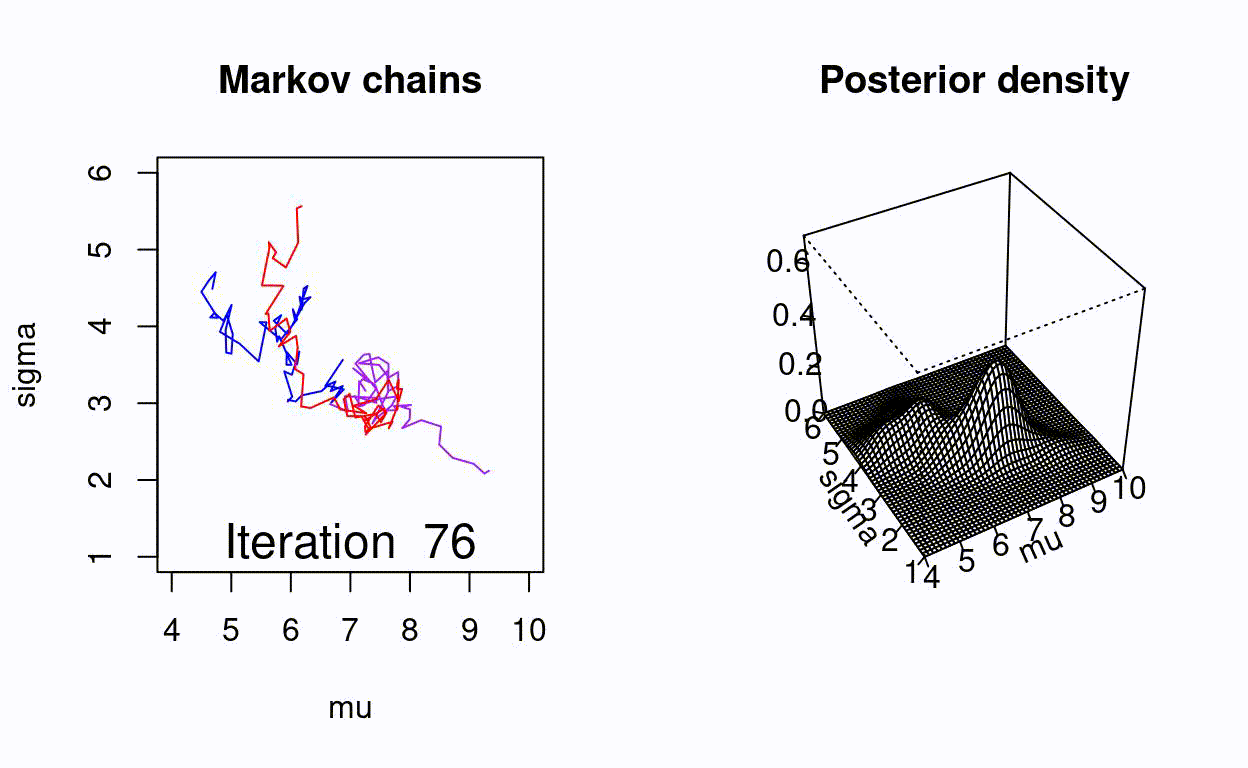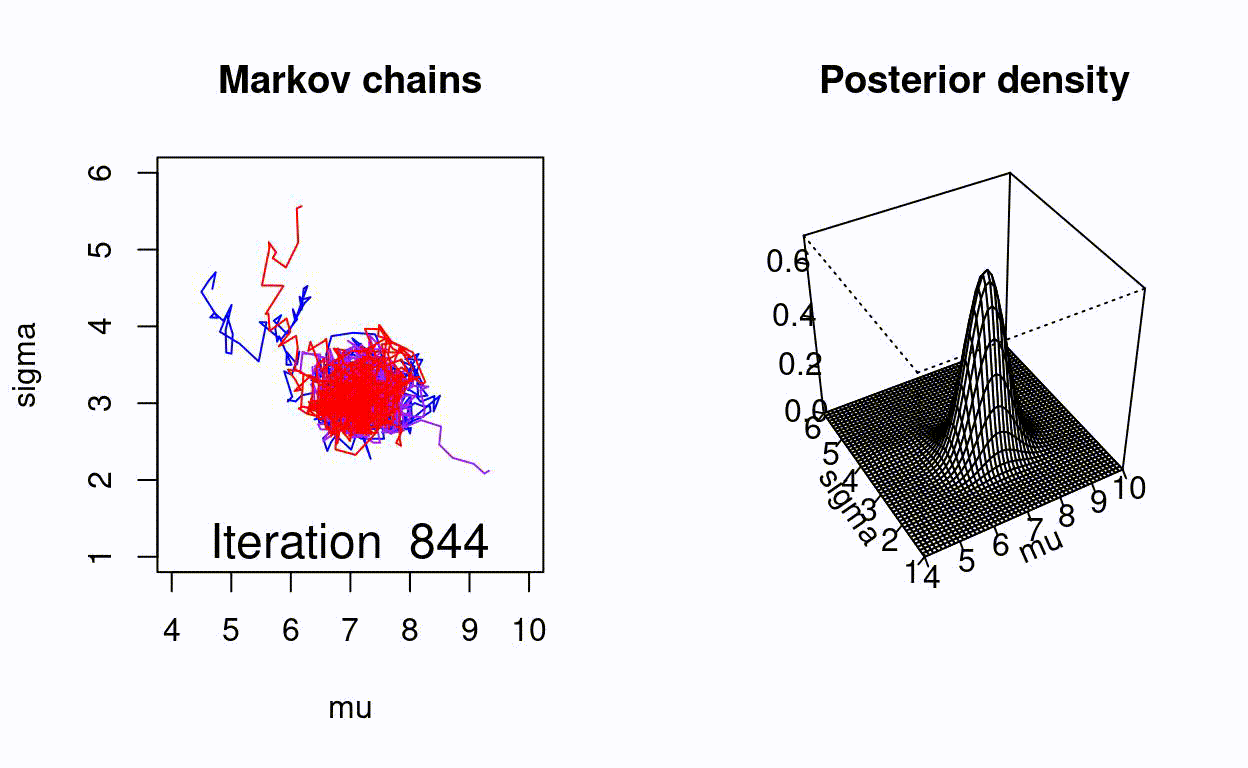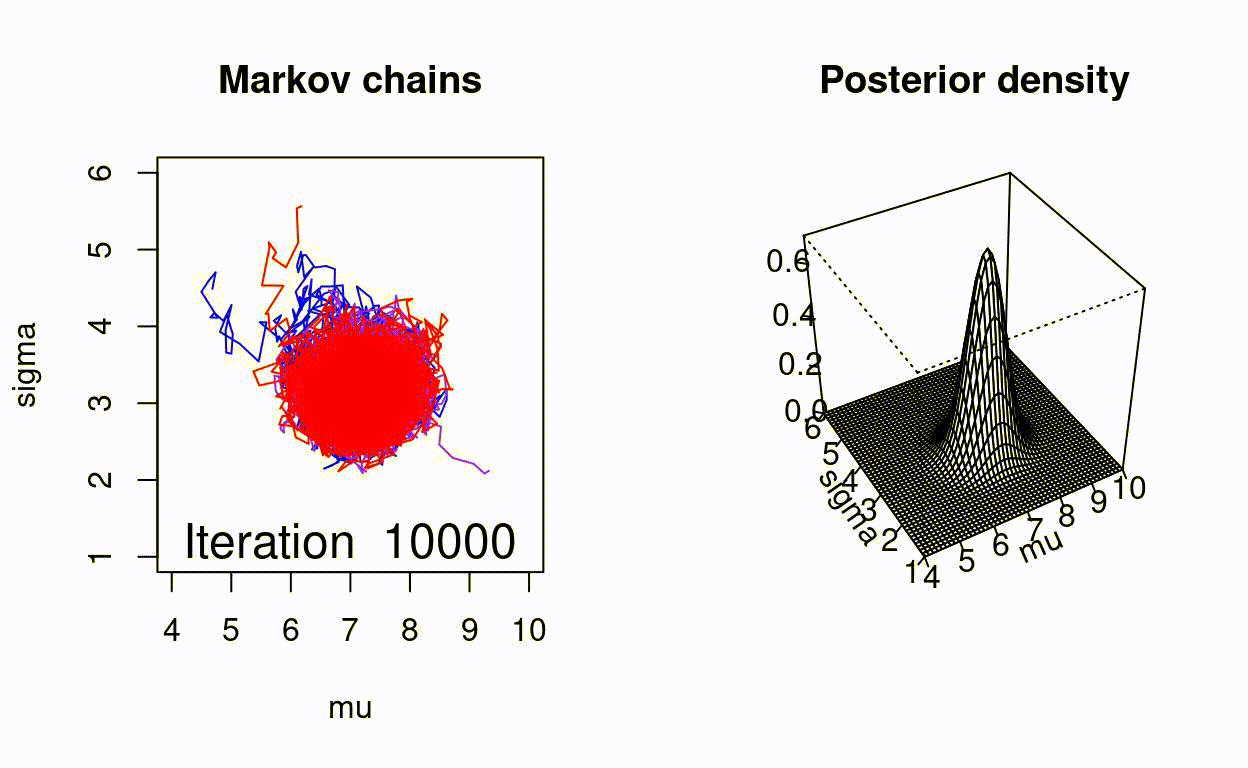
Animating the Metropolis algorithm
A homemade Metropolis algorithm animation using R and the animation package.
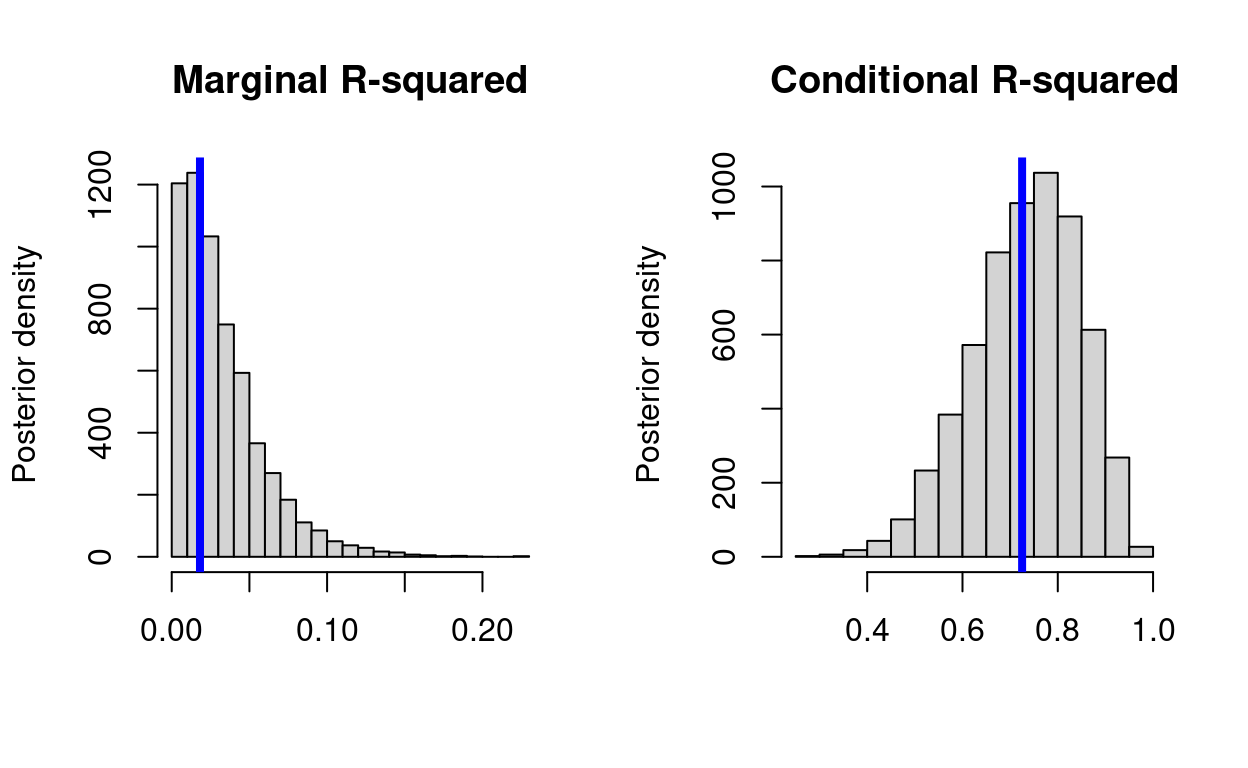
Quantifying uncertainty around R-squared for generalized linear models
How to propage posterior uncertainty to R-squared in R and JAGS.
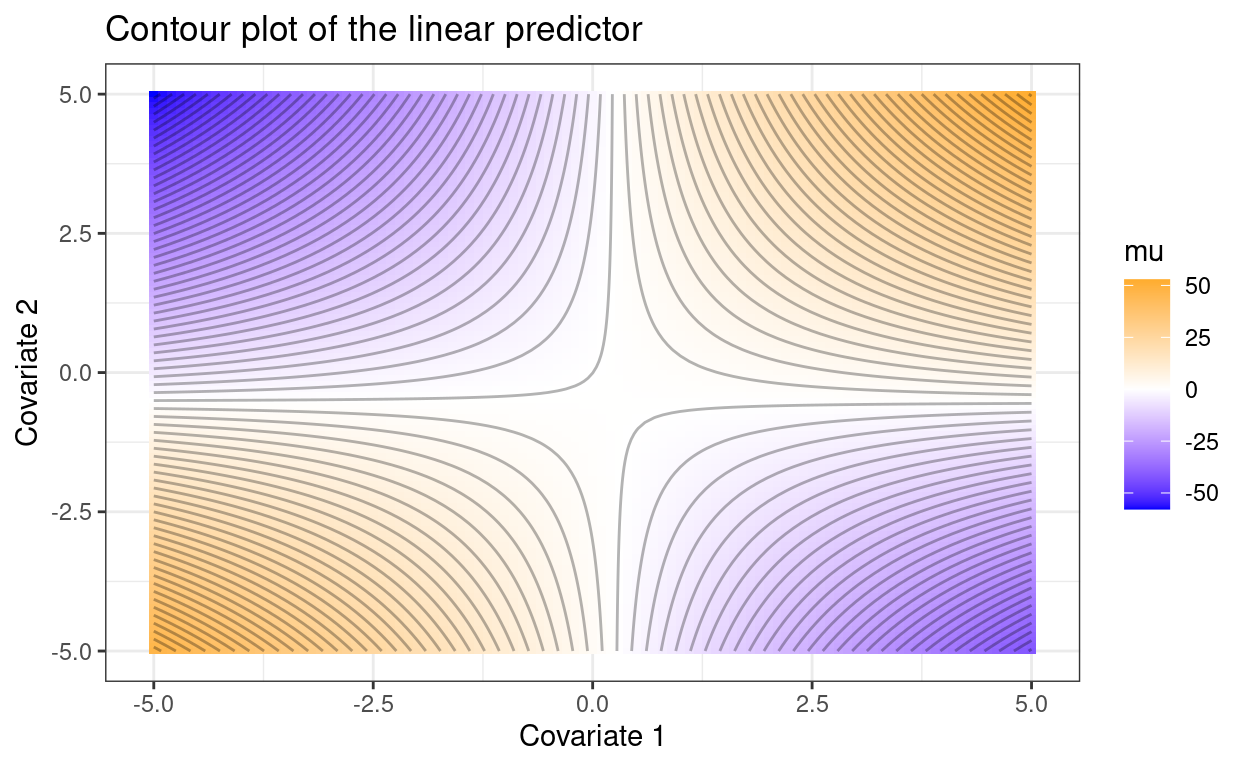
Clarifying vague interactions
One quick way to improve reporting of interaction effects in linear models.
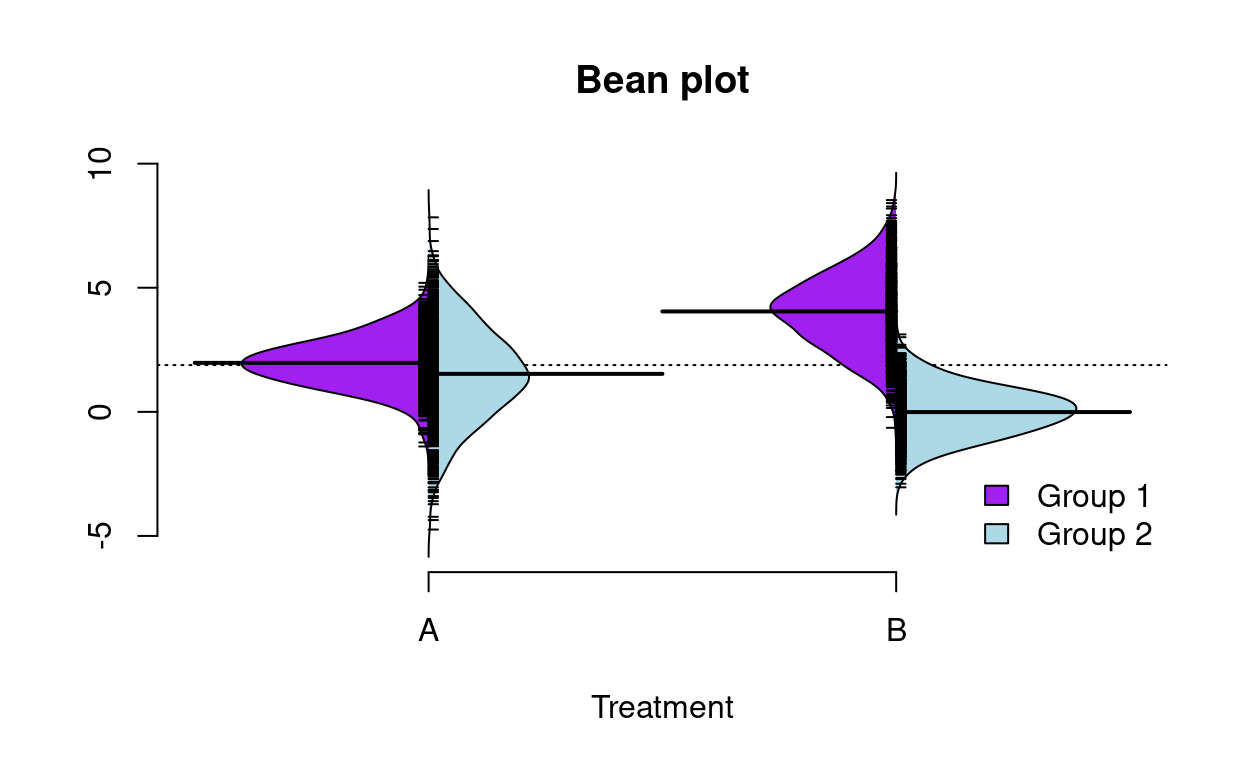
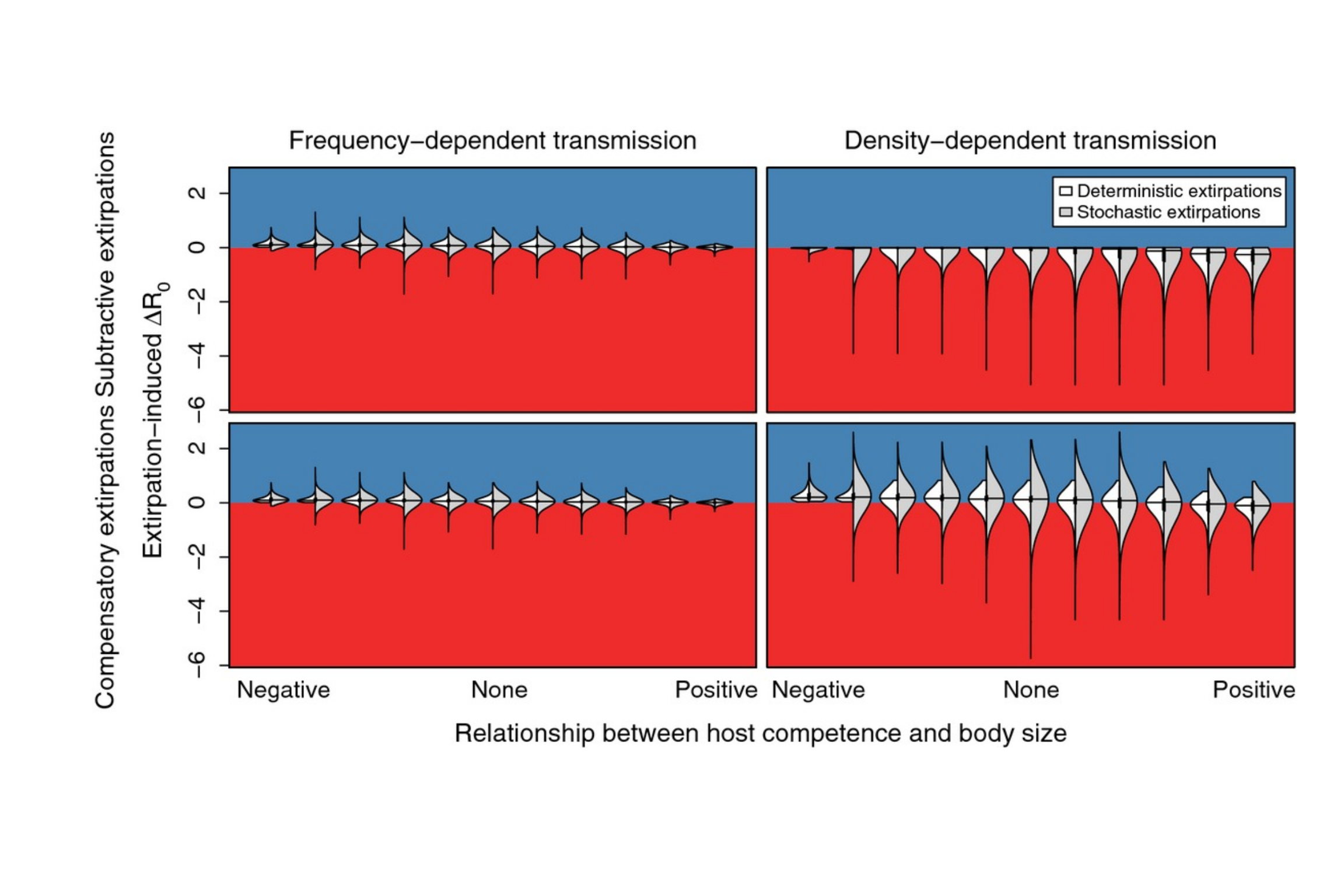
Split violin plots
Comparing distributions with split violin plots in R.
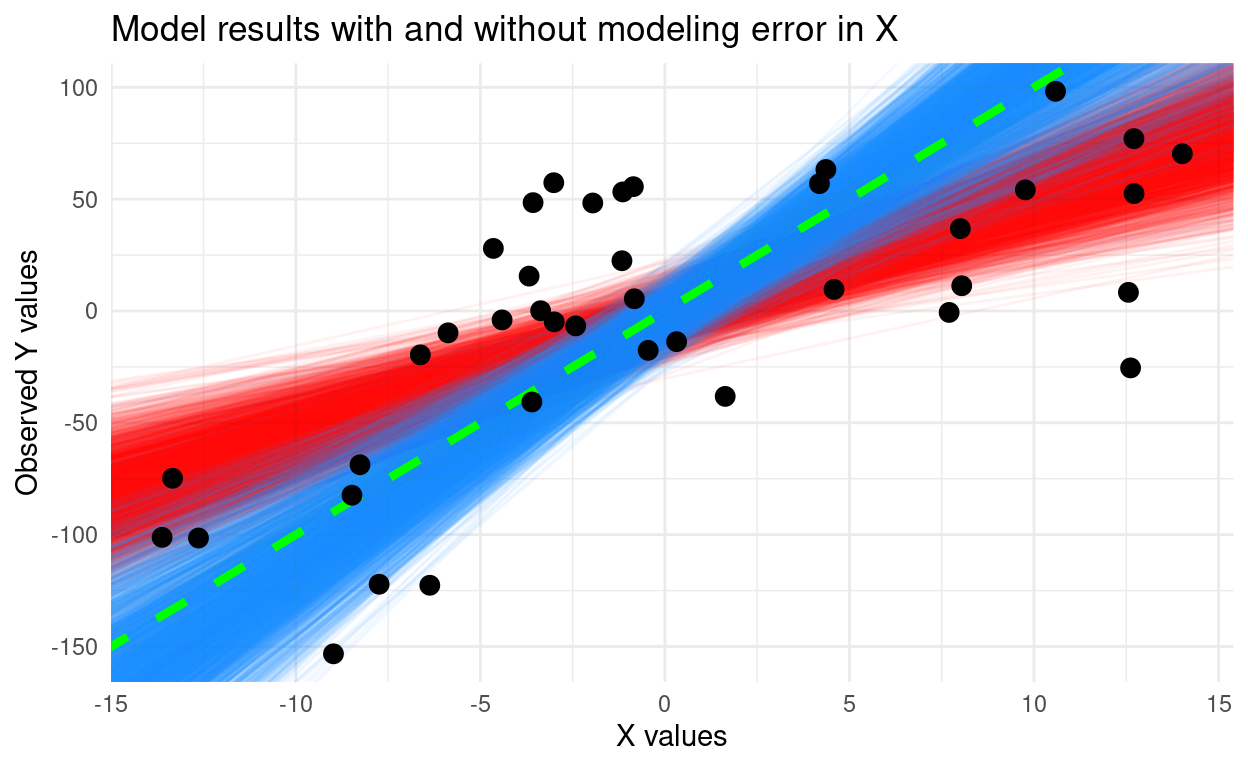
Bayesian model II regression in JAGS
Fitting a regression model with uncertainty in the explanatory variable.
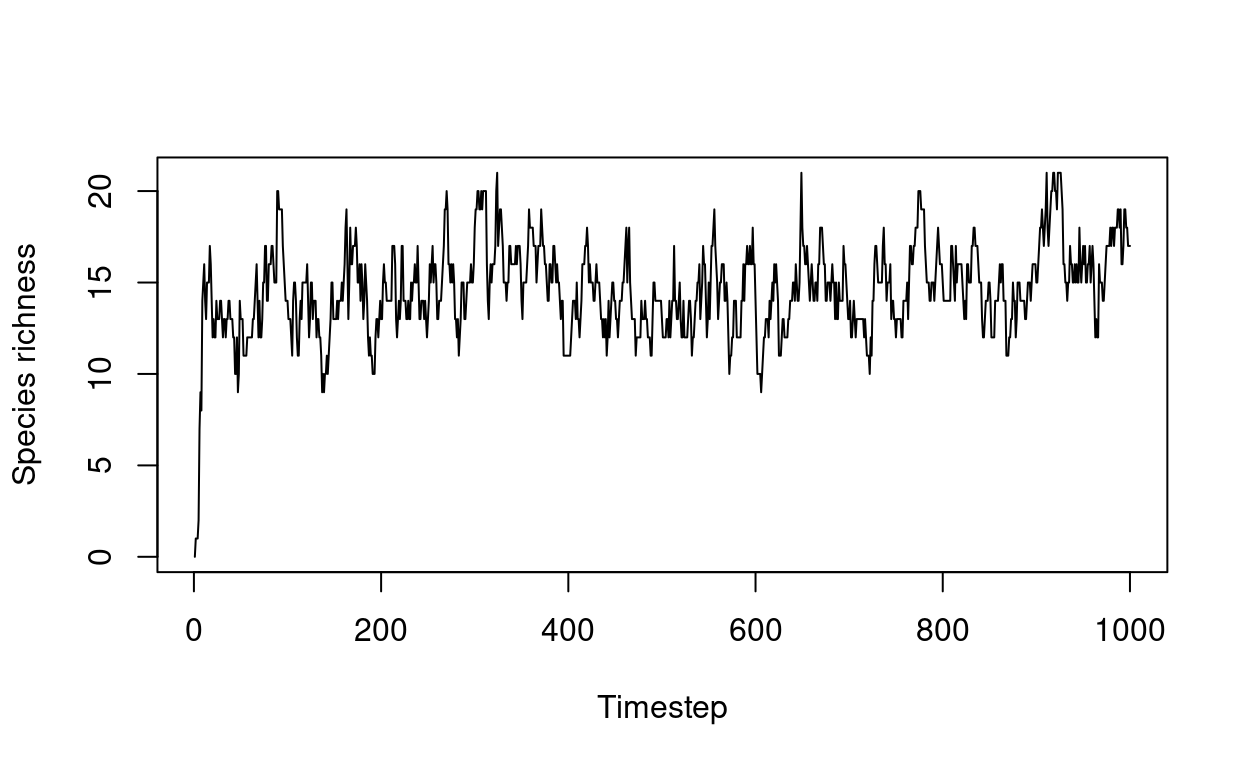
Modeling habitat diversity and species richness
Experimenting with an agent based model of habitat diversity and species richness in R.
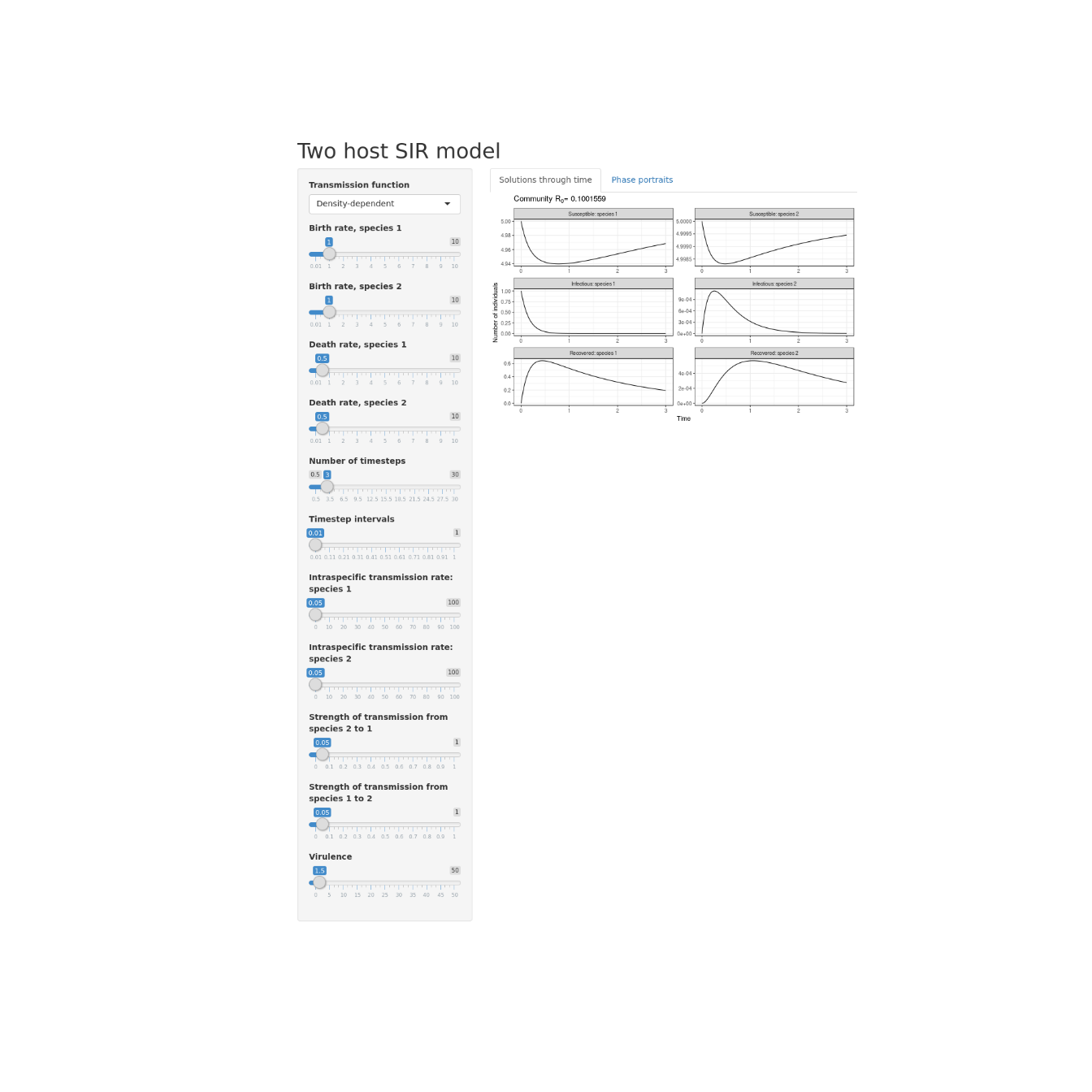
Interactive two host SIR model
Creating an interactive two host SIR model in R and shiny.

Interactive stage-structured population model
Building an interactive stage-structured population model in R with shiny.
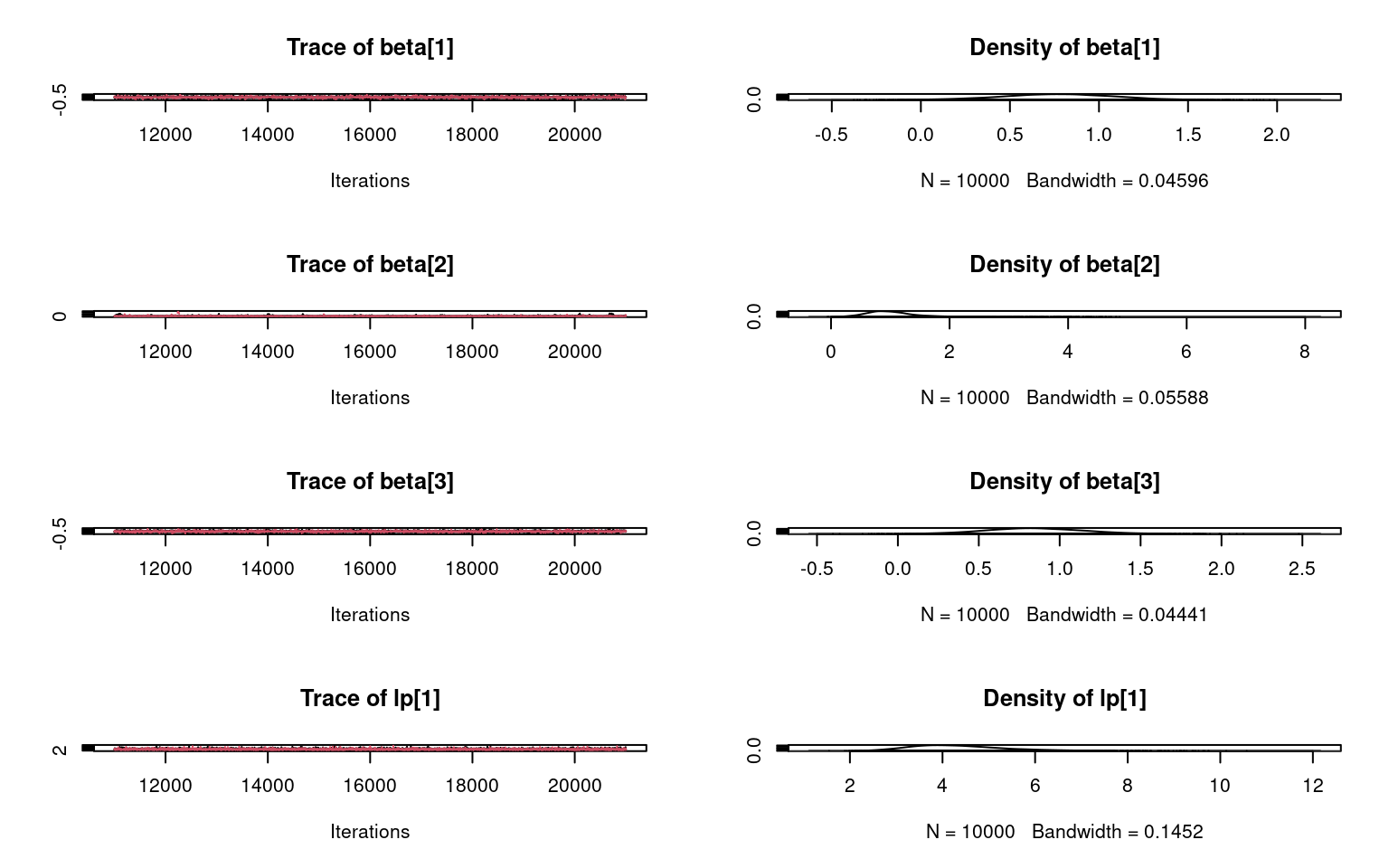
Dynamic community occupancy modeling with R and JAGS
Multi-species, multi-timestep occupancy model in R and JAGS